SGD(1) — for non-convex functions

這一系列文主要要介紹一個非常常用到，幾乎是所有做機器學習、深度學習的人都會知道的方法，Stochastic Gradient Descent (SGD) ，大家幾乎把它當基本常識用，但其實他藏有非常神秘、強大的力量。一開始是實驗做多了大家意外的發現，近幾年才開始慢慢有理論研究給予驗證，雖然結果仍然十分有限，但也足夠我們相信這條路應該還有更多有趣的故事可以發掘。但在這之前要先做一點簡單的背景介紹。

Gradient Descent v.s. Stochastic Gradient Descent

Gradient Descent (GD) 和 Stochastic Gradient Descent (SGD) 是兩個十分相像的演算法，但是表現卻天差地遠。Gradient Descent 顧名思義就是利用函數的 $\bigtriangledown f(x)$ 來往梯度最大的方向走。最顯然的例子就像在山區走，整座山高高低低，如果我們希望最快到山腳，那就會希望沿著最傾斜的方向走。

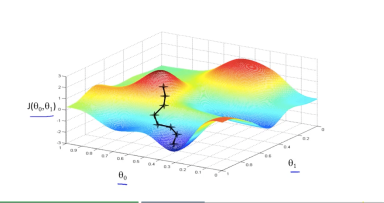
但是大家知道，GD 每當要做一次更新，耗費的計算量很大。因此有另一個改版的更新方式出現，也就是 SGD，他的精神是利用『期望值』的概念，也就是 SGD 只要求走的方向的『期望值』是梯度方向就行了，這樣在夠好的函數上（例如 Convex Function），他仍然有收斂速率的保證（可參考 Shalev-Shwartz 的Ch14）

確切來說， SGD 的做法不需要在每次更新的時候就把所有的 data 看過一次，只要在每個回合﹝iteration﹞隨機從訓練資料 $\mathcal{S}$ 選一筆 $\mathbf{z}$ 出來，然後根據 $\mathbf{z}$ 做 gradient 就行了，﹝但若是 GD 就需要把全部的 $\mathcal{S}$ 都做 gradient 再平均起來﹞這也是大部分的人一開始會使用 SGD 取代 GD 的動機。不過因為是隨機取一筆來做 gradient，想當然的它的行走路徑一定相對 GD 是歪七扭八的，不過總的來說，他最後還是會走到目的地，如下圖所示，圖左是 GD ，圖右是 SGD。

SGD

Non-Convex Function

但是 SGD 的強大並不止於可以做得比 GD 還快，而是我們還發現，他在面對一般的函數也能獲得比 GD 還要好的解。確切來說，一般而言函數是非常複雜的，不會是 convex ，而是 non-convex ；而 neural network 參數量那麼多、又有許多層，整個函數必定是很複雜的，因此此時就很有必要了解為什麼 SGD 幾乎都能夠得到比 GD 好的解。

在這裡簡單介紹 Non-Convex Functions。首先，一般來說解 non-convex function 是一個 NP-hard 問題，例如像是解 4 次多項式函數就已經非常困難。而另外，對於這種 non-convex 函數，我們還必須把『解』定義清楚。也就是說，在 convex function 中，解就只有一個，那就是最低點；但是對 non-convex function 來說就不是這樣了，有所謂的 local minima 和 global minima，例如埔里盆地就是台灣地形的某個 local minima，但他其實不是整個台灣的最低點（global minima），翻過一些山丘後還能繼續往海拔更低處走。整個 non-convex function 很複雜，但是其實在『非水平點』，我們都可以直接沿著 $\bigtriangledown f(x)$ 方向走，麻煩的是如果 $\bigtriangledown f(x)=0$ 時又該怎麼辦？因此現在我們要將目光專注於那些 $\bigtriangledown f(x)=0$ 的那些平衡點（critical points）。

Critical Points

Critical points 其實又可以大致分成三類地形：

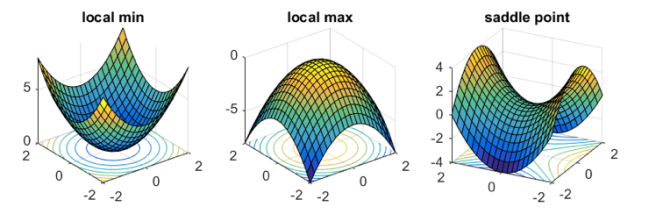
由於這三種地形都是發生在 $\bigtriangledown f(x)=0$ 的時候，因此單靠 $\bigtriangledown f(x)$ 並沒有辦法幫助我們走向更好的解。幸運的是，泰勒展開式告訴我們

$f(y)\approx f(x)+<\triangledown f(x),y-x>+\frac{1}{2}(y-x)^T\triangledown^2f(x)(y-x)$

因此就算 $\triangledown f(x)=0$ ，還可以使用更高次的訊息來幫忙。對於二次項 $\triangledown^2 f(x)$ 來說，有幾個有用的特性：

如果 $\triangledown^2 f(x) \succ 0$ , 則這是一個 local minima
如果 $\triangledown^2 f(x) \prec 0$ , 則這是一個 local maxima
如果 $\triangledown^2 f(x)$ 同時有 $+/-$ 特徵值（eigenvalues），則這是一個 saddle point
而若 $\triangledown^2 f(x)$ 存在特徵值 =0，則可能是 local optimum 或者 saddle point

前兩點狀況相對的來說單純很多，直接用高中的判別方法：二次微分大於（/小於）零則凹口向上（/下），差別只在因為現在 $\triangledown^2 f(x)$ （Hessian）是一個矩陣，所以用 $\succ/\prec$ 這種符號，但概念上是差不多的。那什麼是 saddle point 呢？以地形來說會說他是『鞍部』，也就是在那個點有個特別的特性，他的四周不全然是上坡或是下坡，因此雖然往某些方向走是上坡，但是只要選對方向，還是有機會繼續往低點走的，如圖三右。

Hessian 的特徵值差不多就對應到該處到底是上坡還是下坡，以最終想找到最低點這個目標來說，我們就會希望有多一點負的特徵值，這代表著越多往下的方向，並且希望這些值『很負』，也就代表『很明顯往下』。

Solving non-convex problems

一般來說，就算可以利用 Gradient 或是 Hessian 來幫助得到更好的解，但解 non-convex functions 還是有許多難點，例如：

卡在不好的 local minima
有非常非常多的 saddle points
……

卡在 local minima 十分的麻煩，因爲天曉得在四面的山的背後，有沒有更低的點可以往下走，不像在 saddle points ，至少隱隱約約的還有個缺口可以走。這個問題以後若有機會再詳述。

那至於為什麼會有非常非常多的 saddle points 呢？就算有那麼多的 saddle points 又如何呢？我們不是知道可以往特徵值是負的方向走嗎？『有許多 saddle points』的原因來自於交換對稱（permutation symmetric）。舉個簡單的例子：解 k-clustering 問題。

permutation symmetric：k-means clustering

k-means clustering 的問題是這樣的：假設我是一個老闆，想在一座城市最有效率的蓋 k 間便利商店，請問我該蓋在哪些地方？最有效率意指每間便利商店可以盡量搜集越多顧客、並且彼此不重疊，一個最簡單的想法就是用『距離』分區，而那 k 間便利商店就蓋在那 k 區的中心位置。

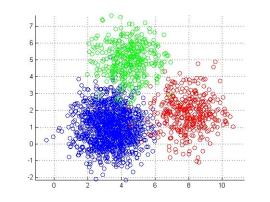
我們用 $(\mathbf{x_1,x_2,\cdots,x_k})$ 這 k 個座標來表達一組解。如果 $(\mathbf{x_1,x_2,\cdots,x_k})$ 這組解是 saddle points ，則很明顯的 $(\mathbf{x_2,x_1,\cdots,x_k})$ ，甚至其他的排列組合也都是 saddle points ，因為他們都代表的某一組位置，只是順序交換了。

上述原因會使得整個 non-convex function 可能有 exponential 多個 saddle points，這讓我們不清楚我們究竟會在 saddle points 迂迴多少次，而最終能不能（快速）收斂到某個 minima。稍微還算幸運的是，對於許多機器學習會面臨到的問題，『所有的 local minima 都是 global minima』（像是 tensor decomposition, dictionary learning, phase retrieval, matrix sensing, matrix completion, $\cdots$ ），這讓我們省掉了一個麻煩。總之，現在只要我們有信心可以逃脫 saddle points ，並且保證可以快速掉到某個 local minima ，那麼問題就解決了。

接下來的文章中，我們會說明 SGD 的確可以有效逃脫 saddle points ，並且證明他的收斂速度（in iterations）。

SGD(1) — for non-convex functions

Gradient Descent v.s. Stochastic Gradient Descent

Non-Convex Function

Critical Points

Solving non-convex problems

permutation symmetric：k-means clustering

[Reference]

發表者：turtleang

發表留言取消回覆

Gradient Descent v.s. Stochastic Gradient Descent

Non-Convex Function

Critical Points

Solving non-convex problems

permutation symmetric：k-means clustering

[Reference]

分享此文：

相關

發表者：turtleang

發表留言 取消回覆

發表留言取消回覆