機器學習可行嗎(3)–Uniform Convergence

經由上一篇<<PAC lernability>>的討論，我們還是沒有辦法說學習真的是可行的，為什麼？因為儘管在上一篇的最後已經把過於理想的Realizability assumption 去除了，但是仍舊有一個不太合理的假設我們還沒解決：我們能在訓練資料上表現地很完美，也就是 $L_S(h)=0$ 。

讓 $L_S(h)=0$ 不好嗎？對，不太好。因為學習的目的是使得 $L_{D,f}(h)$ 越小越好，而不是 $L_S(h)$ 。更糟糕的是， $L_S(h)$ 是我們唯一能夠掌握的判斷依據，我們希望的應該是讓 $L_S(h)$ 能夠忠實反映出 $L_{D,f}(h)$ 的情況，如果真實錯誤率很大，訓練錯誤率也會蠻大；真實錯誤率很小，訓練錯誤率也會很小，這樣才是一個理想的學習吧。

在上一篇中 Agnostic PAC learnable 希望當 $|S|>m_H$ 時， $\mathbb{P}[L_D(h)-min_{h'\in H}L_D(h')\leq \epsilon]\geq (1-\delta)$ 。現在我們希望也能有一個 $m_H^{UC}$ 做為某個標準，只要 $|S|$ 夠大，對於所有在 H 中的 h ，都有 $|L_S(h)-L_D(h)|\leq \epsilon$ ，這件事情跟﹝uniform convergence﹞有些關聯。並且會再說明，如果 H 有 uniform convergence，那我們大概可以說機器學習應該是能夠辦到的﹝agnostic PAC learnable﹞。

Uniform Convergence

說明如下：(討厭證明的話可以跳過用『證明』當開頭的灰色框框)

已知：當 $|S|>m_H$ ，且 $|H|$ 是有限的，會得到 $\mathbb{P}[|L_D(A(S))-min_{h'\in H}L_D(h')|\leq \epsilon]\geq (1-\delta)$ 。也就是這個 H 是 agnostic PAC learnable。

步驟1：定義「好資料」，還記得上一篇說到，取到不具有代表性的資料時會造成誤判，因此我們必須定義「好資料」也就是那些足夠有代表性的資料，意思是演算法在觀察那筆訓練資料後，做出來的預測跟真實錯誤率不會差太多。

定義：代表性的好資料﹝-representative sample﹞
一組訓練資料 S 如果滿足下面條件，則說它是 -representative ：

注意這個定義是對於所有在 H 裡面的 h 都要滿足，是一個非常強的限制。

步驟2：說明如果 S 是「 $\epsilon/2-$ 代表性的好資料」，則用 ERM 學習這筆資料得到的 $h_S$ 會滿足 $L_D(h_S)-min_{h'\in H}L_D(h')\leq \epsilon$ 。

證明：
對於所有 ，
-- 由好資料的定義知道
-- 在 ERM 方法中， 是使得 最小的那個 
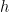
--由好資料的定義知道

由前兩步驟似乎可以看出一點端倪了。如果一個 H 想要得到「已知」當中那個agnostic PAC learnable 的條件，那就表示要有大於 $(1-\delta)$ 的機率 S 是「 $\epsilon/2-$ 代表性的好資料」。

步驟3：想辦法讓 $S$ 有大於 $(1-\delta)$ 的機率是「 $\epsilon/2-$ 代表性的好資料」。也就是讓 $D^m(\{S:\forall h \in H,\quad |L_S(h)-L_D(h)| \leq \epsilon\})>1-\delta$ ，因此剩下的事便是尋找滿足此式的條件。

步驟3-1：
前半部關鍵是現在我們希望找到一個 $|S|$ ，使得用 i.i.d. 從D 中選的 S ，有大於 $(1-\delta)$ 的機率是好資料：
$D^m(\{S:\forall h \in H,\quad |L_S(h)-L_D(h)| \leq \epsilon\})>1-\delta$

或者是相反地，希望小於 $\delta$ 的機率是壞資料：
$D^m(\{S:\exists h \in H,\quad |L_S(h)-L_D(h)| > \epsilon\})<\delta$

而實際上，跟上一篇證明 PAC learnability 用『聯集』的技巧一樣，我們會得到 $D^m(\{S:\exists h \in H,\quad |L_S(h)-L_D(h)| > \epsilon\})$
$\leq \sum_{h\in H}D^m(\{S:|L_S(h)-L_D(h)|>\epsilon\})$

步驟3-2：
後半部要引入Hoeffding 不等式說明：對於任一個在選出 S 前就選定的函數 h，只要 $|S|$ 夠大， $|L_S(h)-L_D(h)|$ 會很小。所以可以得到 $\sum_{h\in H}D^m(\{S:|L_S(h)-L_D(h)|>\epsilon\})$ $\leq 2|H|exp(-2m\epsilon^2)$ ，這就是發生壞資料的上限。

Hoeffding's Inequality 說：
對於一群 i.i.d.選出的資料，如果它們分佈在 a 到 b 之間，且期望值等於 。那麼從裡面任抓一把，只要數量夠大，這些資料的平均很大的可能會很接近期望值。也就是，

我們可以簡單的用「大數法則」來理解Hoeffding 不等式。而有了這個不等式，我們就能完成步驟3-2的證明了。

證明：
我們的問題跟Hoeffding's Inequality有什麼關係？因為訓練資料S是i.i.d.選出來的，所以根據期望值的特性， 正好就是  的期望值。
只要現在讓，並且因為錯誤率界於0、1之間，分別對應到a、b。我們會得到：

 
---Hoeffding's Inequality

最後，要讓 $=2|H| exp(-2m\epsilon^2)<\delta$ ，則會得到 $m\geq \frac{2log(2|H|/\delta)}{\epsilon^2}$ ，這是要讓 $S$ 有大於 $(1-\delta)$ 的機率是「 $\epsilon/2-$ 代表性的好資料」，所需要的最少訓練資料量。而因應了這樣對於「好資料」的要求，我們有了一個定義。

定義：Uniform Convergence Property
如果H滿足下列特性，則說這個 H 有 Uniform Convergence 性質：
H 的大小是有限的，且存在某個 $m_H^{UC}$ ，只要 $|S|\geq m_H^{UC}(\epsilon,\delta)$ ，就會有大於 $(1-\delta)$ 的機率 S 是「 $\epsilon-$ 代表性的好資料」。

這裡的 $m_H^{UC}(\epsilon,\delta)$ 跟上一篇提到的 $m_H(\epsilon,\delta)$ 差不多，都是用來表示滿足該性質所需要的最小資料量。

小結

最後最後做個把 $m_H$ 、 $m_H^{UC}$ 和我們需要達到 agnostic PAC learnable 需要的資料量做的比較，只要稍微多思考一下就會知道：
$m_H(\epsilon,\delta)\leq m_H^{UC}(\epsilon/2,\delta)\leq \frac{2log(2|H|/\delta)}{\epsilon^2}$
也就是說，我們可以觀察到，UC convergence property 是個比PAC learnability 還要強的條件。

總結

由<<PAC learnability>>和本篇的討論知道，我們說一個 Hypothesis H 要是 agnostic PAC learnable 的條件是：要有足夠大的機率，我們選出來的 h 的真實錯誤率會接近該 H 中最小可能造成的真實錯誤率。而在上一章我們知道，要滿足這個條件， $|S|$ 要大於 $m_H(\epsilon,\delta)$ 。
但是知道上面這件事還沒有辦法讓我們學習，因為我們唯一能夠掌握的只有 $L_S(h)$ ，所以進一步的，我們希望在大部分的狀況下 $L_S(h)$ 跟 $L_D(h)$ 也會很接近。而本章告訴我們，要滿足此條件， $|S|$ 要大於 $m_H^{UC}$ 。而當 H 的大小是有限的並且擁有上述條件，那這個 H 就是 agnostic PAC learnable。

機器學習可行嗎(3)–Uniform Convergence

Uniform Convergence

說明如下：(討厭證明的話可以跳過用『證明』當開頭的灰色框框)

小結

總結

[參考資料]
1. Understanding machine learning-from theory to algorithm (Ch4)
2. Learning from data. AMLbook (Ch1)

發表者：turtleang