GAN系列文(2)–Generative Adversarial Nets

這篇要談論的是一個從 2014 年被 Goodfellow 提出來後就十分火紅〈截至三年後的現在已經有1748 次引用〉，並且直到現在已經有數不清種改版的Generative Adversarial Nets，簡稱 GAN。顧名思義，這樣的模型很顯然的是希望機器能夠自己『產生』一些夠真實的東西，像是圖片、影片、甚至文章等等。那這個模型跟以前有的生成模型比起來，到底好在哪裡呢？為什麼會這樣被廣為使用呢？這篇文章將一一說明。

從前從前

從前從前，有另一種常被使用的方式叫做 Auto-Encoder，它的做法是這樣的：如果現在考慮的都是「圖片」，我們希望將這張圖片輸入之後，經過這個模型，模型會輸出另一張圖，而且輸出跟輸入長得越像越好。理論上這件事情只要『複製』再『貼上』就好，也就是如果一個函數 F 輸入一個向量 ( 1 , 3 , 5 )，那我只要輸出 ( 1 , 3 , 5 ) 就完成了。但因為每一張圖片的資訊量是很大的，我們不希望耗費那麼多功夫，而且這般複製貼上根本不是我們希望的，因為沒有辦法產出新的東西，所以我們希望『壓縮碼』( code ) 的維度比原圖片低很多，意思是我們希望『編碼器』( encoder ) 能夠從中擷取『關鍵特徵』，然後『解碼器』( decoder ) 可以有辦法這個『關鍵特徵』盡可能還原圖片。

這樣有什麼好處？就像我們在學畫畫一樣，我們不會把所有看過的東西的所有細節背下來然後照著畫〈某種程度也辦不到〉，我們會在一次一次的描摹當中，慢慢知道怎麼抓特徵然後記錄下來，再根據特徵畫成整張圖〈盡量讓輸入輸出越像越好，最終學會如何編碼、如何解碼〉，例如：狗普遍有尾巴、四隻腳著地、濕濕的鼻子；人是兩隻腳站立等等等。

這是我們學畫畫的方式，希望能夠從「畫的接近」開始然後慢慢的自己能「畫出新的圖」，而我們某種程度也希望機器這樣學。也就是當學好的機器獲得『壓縮碼』後，基本上就能夠根據學好的『解碼器』輸出一張新的圖片。

但這樣的模型有一個缺點，那就是『畫的接近』跟『畫得像真實的圖』某種程度有正相關卻又不那麼直接相關，舉個例子：左右兩個『 1 』唯一不一樣的就是那兩個用紅色標出來的點，如果硬要你選一個，你覺得哪一個看起來比較『真實』？也就是比較像真正被寫出來的 1 ？大部分的情況下我們應該會選擇左邊。但是如果用上一篇《 GAN 系列文 (1) — distance of distribution 》提到的用格子點的方式計算距離，這兩者應該是一樣的。也就是說對這個模型來說兩個數字在『像不像』方面並沒有差別。

AE problem.png — 圖三、兩張圖對 auto-encoder 來說都一樣。

因此是時候想一個更能夠判斷輸出『真不真實』的模型了。

Generative Adversarial Nets ( GANs )

GAN 的發明起源於一個重要的想法：「要靠人為的方式制訂一套規則教機器分辯『真不真實』實在是太難了，對於不同情境，這規則可能寫都寫不完，且會有很多例外。」但我們知道一件事：從「分類問題」( classification problems ) 的經驗，我們發現

觀念一：機器自己就很能夠學習如何判斷、分類，它的分類邏輯可能不是現在我們能夠說清楚講明白的，但卻似乎很有效，那麼，何不讓機器自己學習判斷圖片真不真實呢？

更確實的來說，我們可以想像一個有兩名玩家的遊戲。玩家 Generator 〈簡稱：G 〉是個『生成者』，玩家 Discriminator〈簡稱：D 〉是個『分辨者』，這是個從『 XX 者』變成『 XX 家』的養成遊戲。

圖四、Generator 需要從一堆 noise 中 (通常是 Gaussian distribution) 抽樣一個雜訊 z ，使其通過 G 變成 G(z)。本文中簡單將 G(z) 形成的分布直接當作 $P_{G}$ 。

圖四、Generator 需要從一堆 noise 中 (通常是 Gaussian distribution) 抽樣一個雜訊 z ，使其通過 G 變成 G(z)。本文中簡單將 G(z) 形成的分布直接當作 $P_{G}$ 。

分辨者的目標是要能夠分辨一張圖片 x 是由生成者製造的〈 $x\sim P_{G}$ 〉，還是來自真正的圖片集〈 $x\sim P_{real}$ 〉；而生成者的目標是要能想辦法吐出一個「夠真實的圖片」騙過分辨者，也就是要想辦法讓產出圖片的分布 $P_{G}$ 越接近 $P_{real}$ 越好，而顯然地獲勝的只有一個。這個遊戲以「回合」方式進行，一開始雙方都很弱，一個亂產生〈兩個分佈根本八竿子打不著〉，一個亂分辨〈以幾乎一半一半的機率亂猜〉，但是越到後來，隨著

$D_1$ 想辦法分辨 $G_0$
$\rightarrow G_1$ 想辦法騙過 $D_1$
$\rightarrow D_2$ 想辦法分辨 $G_1$
$\rightarrow G_2$ 想辦法騙過 $D_2$
$\cdots$

他們將會越學越好。

寫到這裡，不知道會不會有人困惑，像這種『想讓分佈 A 接近分佈 B』的事情，為什麼不用機器學習較常見的 maximum likelihood 的方法，而要用這種兩個玩家玩遊戲的方式刻畫問題呢？

Maximum likelihood 的困難點

maximum likelihood 簡而言之就是：

如果今天手上有一組真實資料〈訓練資料〉 $\{x_1,x_2,x_3,\cdots, x_m\}$ ，它們是從真實分佈 $P_{real}$ 中抽樣出來的，那怎麼尋找最接近 $P_{real}$ 的分佈 $P_{G}$ 呢？很簡單，就是找能最大化產生 $\{x_1,x_2,x_3,\cdots, x_m\}$ 這組資料的機率的函數。在這裡需要把 $P_{G}$ 考慮得更詳細一點，也就是像「圖四」中描述的，Generator 需要從一個 noise distribution (Z) 中 (通常是 Gaussian distribution) 抽樣一個雜訊 z ，使其通過 G 變成 G(z)，且 $G$ 是一個以 $\theta$ 為參數的類神經網路，也就是調整不同的 $\theta$ 就會對應到不同的 Generator。

如果將 Likelihood 訂為〈；後表示是函數 G 的參數〉：

$L=\Pi_{i=1}^m P_G(x_i; \theta)$

因此學習的目標就是找一個 $\theta^*$ 最大化 $L$ 。由很制式的算法能夠得到：

$\theta^*=arg\max_\theta \Pi_{i=1}^m P_G(x_i; \theta)$

$=arg\max_\theta log[\Pi_{i=1}^m P_G(x_i; \theta)]=arg\max_\theta \sum\limits_{i=1}^m log[ P_G(x_i; \theta)]$

$\approx arg\max_\theta \mathbb{E}_{x\sim P_{data}} log[ P_G(x; \theta)]$ — (1)

$=arg\max_\theta\int_x P_{data}(x)log[ P_G(x; \theta)]dx-\int_x P_{data}(x)log[ P_{data}(x)dx]$ — (2)

$=arg\min_\theta D_{KL}( P_{data}(x)||P_G(x; \theta))$ — (3)

從式 (1) 到式 (2) 多減了後面那一項，但是它跟 $\theta$ 無關，因此不影響 $\theta$ 的最佳值。而從式 (2) 到式 (3) ，我們將會很興奮的發現這其實就是在《GAN系列文(1)》介紹到的 KL divergence，也就是這個 $\mathbf{\theta}$ 最終的目標就是最小化 $\mathbf{P_{data}(x)}$ 和 $\mathbf{P_G(x; \theta)}$ 的 KL divergence，這個推導結果很符合直觀。

到這裡看起來很順利，不過往往都是這樣，在最順利的時候麻煩也就來了。因為 $P_G(x; \theta)$ 是一個很複雜的 neural network ，也就是對於每一筆看到的資料，我們要計算它從 $P_G(x; \theta)$ 中抽樣的機率：

$P(x)=\int_z P_{Gaussian}(z)I_{G(z)=x}dz$

就算我已經明明白白地寫下 $z$ 就是從 Gaussian distribution 取出的，但後面還有一個 Identity function ，這使得要計算 maximum likelihood 變得困難。因此才會使用上面提到的「玩遊戲的方法」，或是稍微專業一點點的說法：「對局」的方法。

對局方法 ( Game )

姑且就將這個標題訂為對局方法。這個方法為什麼行的通呢？這起因於一個很重要的想法：〈雖然這個想法在今年被質疑了，但實務上 GAN 仍然是做的最不錯的模型〉

觀念二：只要能夠訓練出一個夠好的分辨者 ( discriminator ) ，則就能夠利用它給生成者 ( Generator ) 一些回饋 ( Gradient feedback )，使得生成者能夠進步。

這件事情直觀上是很合理的。如果有一個夠好的老師，你每畫一張畫，他就告訴你畫得夠不夠真實、並且還告訴你什麼樣是可能的修改方向，那豈不是很棒！對於 G 來說，目標函數就可以寫成：

$G^*=arg \min_G\max_D V(G,D)$ — (4)

而 $V(G,D)=\mathbb{E}_{x\sim P_{data}}[log(D(x))]+\mathbb{E}_{x\sim P_G}[log(1-D(x))]$ –(5)

這兩條式子，又 min 又 max 的，且 $V(G,D)$ 又很長，乍看之下很複雜，但其實也沒那麼複雜。先別管 (5) 來看看 (4) 就好。引用一張台大李宏毅老師的投影片就很清楚是怎麼回事了。

先固定外層的 $G$ ，對每個 $G_i$ 都做出 $D\mbox{ v.s. }V(G_i,D)$ 的關係圖，又因為 $D$ 是 max 的下標，因此對 $D$ 而言，他希望可以最大化這個值， $V(G,D)$ 。因此對每個 $G_i$ 都挑出最大的 $V(G_i,D)$ ，也就是圖中的紅點。
處理完 $D$ 後，接下來因為 $G$ 是 min 的下標，因此最好的那個 $G^*$ ，其實就是擁有最小紅點值的 $G$ ，在這個例子中就是 $G_3$ 。

那究竟 Discriminator 是希望什麼值能越高越好，而 Generator 是希望什麼值越低越好呢？ $D$ 輸出的值介於 0 和 1 之間，它希望給真實的圖 ( $x\sim P_{data}$ ) 越高的分數越好，並希望給假的圖 ( $x\sim P_G$ ) 越低的分數，它的目標就是做好這個評分工作。可以發現理想情況是 $D$ 給每個真實的圖片 1 分，並且給每張假的圖片 0 分，這樣整個 $V(G,D)$ 就會最大；反過來地， $G$ 的目標當然就是希望製造出可以『以假亂真』的圖片使得 $D$ 誤判，讓 $V(G,D)$ 降下來。這就是式 (5) 要說的事情。

計算最佳的 $D^$ 、 $G^$

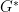
最好的 D：

講到這裡總算要來看到底怎麼樣的 G、D 最理想了。同樣地先固定 G，則要求 D 的最大值透過一次微分積分裡的函數就能得到。

$(5)=\int_x [P_{data}(x)log[D(x)]+P_{G}(x)[log[1-D(x)]]]dx$

$\Rightarrow D^*(x)=P_{data}(x)/(P_{data}(x)+P_{G}(x))$

這個結果其實也很直觀，固定一個 $G$ ，對於某一筆資料，最理想的 $D$ 理論上會給它的分數，就是它有多少機率會是從真實資料中取出的。

最好的 G：

根據上面的《觀念二》，當我們擁有一個夠好的 discriminator 的時候，則它給的回饋就能使 Generator 進步。那到底要進步到什麼程度呢？又或者是問說目標是什麼？我們同樣要用理論的方法分析這件事。

因為現在已經有一個最好的 $D^*(x)=P_{data}(x)/(P_{data}(x)+P_{G}(x))$ 了，因此可以將 (4)、(5) 改寫成：

$G^*=arg \min_G\max_D V(G,D)=arg \min_G V(G,D^*)$ — (4′)

$V(G,D^*)=\mathbb{E}_{x\sim P_{data}}[log\frac{P_{data}(x)}{P_{data}(x)+P_{G}(x)}]+\mathbb{E}_{x\sim P_G}[log\frac{P_{G}(x)}{P_{data}(x)+P_{G}(x)}]$ –(5′)

對分子分母同除以二並不影響結果，但是可以讓我們等下得到更漂亮的表示式，因此

$V(G,D^*)=-2log(2)+ \int_x P_{data}(x)[log\frac{P_{data}(x)}{(P_{data}(x)+P_{G}(x))/2}]+\int_x P_{G}(x)[log\frac{P_{G}(x)}{(P_{data}(x)+P_{G}(x))/2}]$

而如果現在又令 $M(x)=(P_{data}(x)+P_{G}(x))/2$ ，則

$V(G,D^*)=-2log(2)+ \int_x P_{data}(x)[log\frac{P_{data}(x)}{M(x)}]+\int_x P_{G}(x)[log\frac{P_{G}(x)}{M(x)}]$

很幸運的，這就是在《GAN系列文(1)》中介紹的 JS divergence，

$V(G,D^*)=-2log(2)+JSD(P_{data}(x)||P_{G}(x))$

最後最後，最好的 $G$ ：

$G^*=arg \min_G V(G,D^*)$

$=arg \min_G [-2log(2)+JSD(P_{data}(x)||P_{G}(x))]$ –(6)

也就是要去最小化 $P_{data}$ 和 $P_{G}$ 的 JS divergence，又這個 JS divergence 的範圍是：

$0\leq JSD(P_{data}(x)||P_{G}(x))\leq log(2)$ (以 e 為底的範圍)

什麼時候會等於零？也就是當

$P_{G}(x)=P_{data}(x)$

演算法

有了那麼多的理論分析後，現在可以來看看 GAN 這個模型到底是怎麼訓練的了！

這個演算法有幾個可以注意的地方：

generator 和 discriminator 的 gradient 目標都是根據前面討論的目標函數決定的。
k 代表了希望每訓練幾次 discriminator 後才訓練一次 generator 。為什麼要這樣呢？前面談到，一個「夠好的」discriminator 可以督促 generator 學得好，因此這個參數或許需要經過仔細調整，讓 discriminator 跟 generator 的訓練速度可以互相追趕，達到目的。
這裡的 gradient updates 使用的是 momentum 。

之所以特別把這些列出來，是因為這些地方有很多有問題的點，可以參考本文最後「 GAN 在實務上的問題」，以及下一篇文章《GAN系列文 (3)》。

小整理

GAN 的目標函數是：

$\min_G\max_D \mathbb{E}_{x\sim P_{data}}[log(D(x))]+\mathbb{E}_{x\sim P_G}[log(1-D(x))]$

而最佳的 discriminator 是：

$D^*(x)=P_{data}(x)/(P_{data}(x)+P_{G}(x))$

當手上握有那麼好的 discriminator 時，Generator 的目標就是去最小化 $P_{data}$ 和 $P_{G}$ 的 JS divergence。又理想上，最小值發生在當

$P_{G}(x)=P_{data}(x)$

GAN 的問題

理論分析的部分到這裡告一個段落，這個方法看起來十分合理，最好的情況當然就是 Discriminator 可以很好地分辨真偽，然後進一步促使 Generator 提升產出圖片的品質，不過這裡仍就有許多問題，其中幾個比較顯然的：

我們很直接地就假設了 Discriminator 能到達到某個很好的點，且 Generator 也有一個最好的狀態，也就是這個遊戲存在一個『平衡點』，但這在一個兩個玩家的遊戲中並不是那麼顯然會成立的。舉一個最簡單的例子：剪刀石頭布，這個遊戲並沒有一個平衡點，很多方式都會贏，也很多方式都會輸、獲是和局。因此這樣的假設很直覺但卻是需要被質疑的。
以 GAN 的目標而言，我們似乎很直接的就覺得，如果有一個『最好的 D』，而我們只要能夠讓 $P_{G}(x)$ 盡可能接近 $P_{data}(x)$ ，那麼無論如何 G 就可以成功騙過 D。也就是，我們很自然的就假設遊戲玩到最後， Generator 一定可以贏過 Discriminator，而這件事在有無限多筆訓練資料的時候根據上述的分析可能是成立的，但是實際上當沒有那麼多筆訓練資料時，還會成立嗎？
接續上一點，在沒有那麼多筆資料的時候，就算 Generator 真的幾乎都贏，那『贏了』就代表了『 $P_{G}(x)\approx P_{data}(x)$ 』嗎？會不會當沒有那麼多筆資料時， Discriminator 其實也學得不夠好，而根本無法促使 $P_{G}(x)\approx P_{data}(x)$ 呢？

這些問題將在往後《GAN系列文 (4)》及《GAN系列文 (5)》好好探討。

而另外其實實務上 GAN 也有許多問題，像是：

訓練困難、不穩定。也就是 discriminator 跟 generator 學習的速度如果不好好控制，就會失控，也就是可以想像某一方能力太強大到另一方完全無力追趕。
Discriminator 和 Generator 的 loss 沒有辦法充分顯示這個遊戲到底玩得如何了。回想之前的機器學習問題，我們都可以透過觀察某個 loss ，它會隨著 iteration 慢慢的下降，下降到幾乎不會進步時，我們就知道訓練得差不多了。但在 GAN 的訓練中，(6) 式的 loss 很早就維持在 $2log(2)$ 沒有動，但其實訓練還在繼續，我們無法透過一個標準有效的監控學習的進程。
Generator 產生的樣本雖然真實，但缺乏多樣性，也就是當生成很多很多圖片後，會發現有某一些是非常像的，這是我們非常不希望的。

而這些問題將在往後《GAN系列文 (3)》好好探討。