GAN系列文(4)–Generalization and Equilibrium in GANs

這篇文章基本上延續了《GAN系列文(2)–Generative Adversarial Nets》對於 GAN 這個模型的研究。先稍微對 GAN 的幾個重要結論做個小複習：

GAN 的目標函數是：

$\min_G\max_D \mathbb{E}_{x\sim P_{data}}[log(D(x))]+\mathbb{E}_{x\sim P_G}[log(1-D(x))]$ — (1)

而最佳的 discriminator 是：

$D^*(x)=P_{data}(x)/(P_{data}(x)+P_{G}(x))$ — (2)

當手上握有那麼好的 discriminator 時，Generator 的目標就是去最小化 $P_{data}$ 和 $P_{G}$ 的 JS divergence。又理想上，最小值發生在當

$P_{G}(x)=P_{data}(x)$ — (3)

本篇的主軸會放在回答那一篇文章最後提問的部分問題：

當訓練資料不夠多時、或是當 discriminator 的類神經網路不夠強大時，整個訓練過程還會有一個平衡點 ( Equilibrium ) 嗎？（類神經網路其實也是有很多的參數去調控的，當參數量不夠多時，網路的可調性也受限，此時就不一定能有 $D^*$ 那麼好的 discriminator 了。）
若真有一個平衡點，那一定會是 Generator 贏過 Discriminator 嗎？
Generator 贏過 Discriminator 時，就表示 $P_G\approx P_{real}$ 嗎？

Generalization

在上述對 GAN 的分析中，有兩項後來受到質疑的關鍵假設：

有足夠多的訓練資料可以去逼近、或是估計目標函數 [ 式 (1) ]
假設實際上 Discriminator 的可調參數量有 n 個。則這 n 個參數所構成的 Discriminator 的集合，真的大到有辦法挑到 $D^*$ 這個理想的 Discriminator

首先，不知道讀者還記不記得《機器學習可行嗎 (3)– uniform convergence》的重點？總之就是我們 i.i.d. 的取 m 筆訓練資料，然後希望只要 m 夠大，對這 m 筆資料的估計就已足夠代表真實情況。也就是

$Pr[|\frac{1}{m}\sum\limits_{i=1}^m l(x_i) - \mathbb{E}_{x\sim D} l(x)|\leq \epsilon]\geq 1-\delta$

這就是 generalization 。從估計手上握有的情況，推展到真實情況。而 GAN 的目標也是希望能夠使得 $P_{G}$ 足夠接近 $P_{real}$ ，因此很自然的我們會希望用差不多的方式刻畫，於是有了以下的定義：

定義：（generalize）
給定 m 個從 $P_{real}$ 取出來的資料，它們形成分佈 $\hat{P}_{real}$ 。如果一個 distribution $P_{G}$ 滿足以下條件，那就說這個 $P_{G}$ 在這個距離定義下， $d(\cdot,\cdot)$ ，可以被 generalize：

$Pr[|d(P_{real},P_{G})- d(\hat{P}_{real},\hat{P}_{G})|\leq \epsilon]\geq 1-\delta$

這裡 $\hat{P}_{G}$ 指的是從 $P_{G}$ 取出來的 $m$ 筆資料形成的分佈。要特別注意的是 $m$ 的數量要能在 polynomial time 的時間內跑完。 ¤

在這個定義中， $d(\hat{P}_{real},\hat{P}_G)$ 是我們能掌握的，且希望能由這個推估真正的距離 $d(P_{real},P_{G})$ 。但並不是任意一種距離函數 $d(\cdot,\cdot)$ 都能被 generalize ，也就是說，不是所有函數，當你觀察到機器產生 m 筆資料的分布 $\hat{P}_G$ 跟從真實分佈中取 m 筆資料的分佈 $\hat{P}_{real}$ 很接近時，他們之間的真實距離會真的很接近。

這件事情為什麼重要，因為在這篇論文發表以前，所有跟 GAN 有關的模型討論的距離函數，不外乎就是 JS divergence、KL divergence，或是 Wasserstein distance。（關於這些距離，可以參考《GAN 系列文 (1) 》）但非常不幸的，這些距離在 $m$ 的數量如此受限下，都不能 generalize！！

例子：現在有 $\mu, \nu$ 兩個平均值和標準差都一樣的 Gaussian distributions 。假設 $\hat{\mu}$ 是從 $\mu$ 中取 m 筆資料形成的分佈，而 $\hat{\nu}$ 則是從 $\nu$ 取，這裡的 m 同樣只有 polynomial 多個。則很顯然的，無論是計算 JS divergence 還是 Wasserstein distance ， $d(\mu,\nu)$ 都是零，因為它們根本就一樣；但是有很高的機率 $d(\hat{\mu},\hat{\nu})$ 卻不是，因為很少的點並不足以完全描繪出這個 distribution，因此這兩個距離都不能被 generalize。

$d_{JS}(\mu,\nu)=0,\quad d_{JS}(\hat{\mu},\hat{\nu})=log2$
$d_{W}(\mu,\nu)=0,\quad d_{W}(\hat{\mu},\hat{\nu})\geq 1.1$ ¤

為了克服這個麻煩，因此又有了另一個距離的定義產生：

定義：（Neural net distance）
對於兩個 distribution $\mu,\nu$ ，定義 Neural net distance 為

$d_F(\mu,\nu)=sup_{D\in F}\mathbb{E}_{x\sim \mu}[D(x)]-\mathbb{E}_{x\sim \nu}[D(x)]$

而 $F:=\{D_v,v\in V\}$ 是一群滿足 L-lipschitz w.r.t. $v$ （如果兩個 discriminator 的參數距離很近，那兩個 discriminator 的表現差不多）、且只有 n 個可調參數的 neural nets。另外還有一個使這個距離可以被 generalize 的關鍵： $V$ 是緊緻集合 ( compact set )。 ¤

Neural net distance 可以被 generalize 直觀上的理由可以想成：
整個 discriminator 的集合雖然很大，但其實看其中有限多個 discriminator 就已經足以代表全部 discriminator 的行為，但是很不幸的，只要 $m\geq O(\frac{n log(n)}{\epsilon})$ ，就有很高的機率，這些有限個 discriminator 無法分辨 $\mu$ 和從 $\mu$ 中取 m 筆資料形成的分佈 $\hat{\mu}$ 。

更詳細地說：

如果 $D_{v1}$ 跟 $D_{v2}$ 對於同一筆資料 $x$ 給出的結果其實幾乎一樣，那就可以將它們劃分為『同一種 discriminator』（L-lipschitz w.r.t. $v$ 保證了這件事），且更好的是其實只要有『有限多個』不同種的 discriminator ，就足以代表所有 discriminator 的行為了（compact 保證了這件事）。
因為這些 discriminator 只有 n 個可調參數，因此如果有兩個分佈： $\mu$ 、 $\hat{\mu}$ ，只要 m 夠大〈 $O(\frac{n log(n)}{\epsilon})$ 〉，有很高的機率，所有這些有限個 discriminator 都沒有辦法分辨 $\mu$ 和 $\hat{\mu}$ 。

Generalization v.s. Diversity

從上面的討論可以得到一些重要的觀察，這大概也是這一節最重要的事情，如果前面都看不懂只要記得這些就好 (?)：

我們說 generator 會『贏』 discriminator ，指的是，discriminator 對任何一筆資料的預測都跟用 1/2 的機率亂猜沒什麼兩樣。
$m$ 要取多大只跟 discriminator 的大小 $n$ 和要求的精確度 $\epsilon$ 有關。
$m$ 只要取大約 $O(\frac{n log(n)}{\epsilon})$ ，discriminator 就無法分辨這個分佈到底是連續的 $\mu$ 還是只有 m 個 support 〈有點像是線性代數的 basis 的概念〉的 $\hat{\mu}$ 。
取更多的 sample 其實對 training 沒有太大的幫助〈這是很違反傳統機器學習的直覺的！〉，因為無論如何 discriminator 都沒有辦法分辨。
既然 discriminator 的能力那麼受限於 n ，連 generator 到底只學到了 $\hat{\mu}$ 還是已經學會完整的 $\mu$ 都無法分辨，那身為一個懶惰的學習者，當然只要學會 $\hat{\mu}$ 可以騙過 discriminator 就好了啊！因此就算 generator 已經贏過 discriminator 了，可能也只達到 $P_{G}\approx \hat{P}_{real}$ ，而不是理想中 $P_{G}\approx P_{real}$ 。generator 可能根本還學不到真正的分佈，也就是 generator 產生的圖的 diversity 可能不夠！

針對第 4 點，因為這純粹是理論上說它『可能發生』，但不一定真的就發生了，因此幾個月後 Arora 給出了實驗上的證明，證明真的發生了！這也是《GAN 系列文 5》要說的。

Equilibrium

但講到現在我們都還沒回答「為什麼最後一定是 generator 會贏？」這個重要的問題。

Game theory

在回答這個問題之前，需要用到一點點賽局理論，並且要先好好定義什麼是『平衡點』 ( Equilibrium )。對於每個遊戲，都有一個 payoff function，在我們的討論中，這個其實就是我們 (1) 式中要去 min max 的那個函數。所謂的『平衡點』，其實就是：

當玩家 1 選定了一個他最好的策略，然後玩家 2 再根據玩家 1 的策略選擇對他自己最好的策略；反過來，當玩家 2 選定了一個他最好的策略，然後玩家 1 再根據玩家 2 的策略選擇對他自己最好的策略。如果兩種方式玩出來的解都一樣，那就說這個遊戲有『平衡點』。

在賽局理論中，一個 2-player game 「可能」會不存在這樣的『平衡點』。而很不幸的，我們原本 GAN 的架構就是依個 2-player game。而實際上，在 Goodfellow 在 2016 NIPS 會議上就有提到，現在實務上 GAN 在訓練的時候，常常會有「震盪」的情形。而這個震盪造成的最大的麻煩，就是所謂的『Mode collapse』，或有人稱『Helvetica scenario』，簡單來說就是 generator 可能會將很多不同的輸入， $z$ ，通通都給出一樣的輸出。

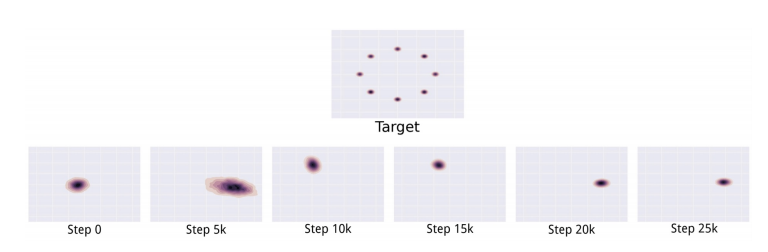
mode collapse.png — 圖一、Mode collapse 示意圖 [3]。上面的 target 是真正的 $p_{data}$ ，下排的圖從左到右，分別是 GAN 經過不同的訓練時間學到的東西，可以發現它並沒有把真正的 distribution 學下來，而是在不同的可能的點中不斷震盪。

圖一、Mode collapse 示意圖 [3]。上面的 target 是真正的 $p_{data}$ ，下排的圖從左到右，分別是 GAN 經過不同的訓練時間學到的東西，可以發現它並沒有把真正的 distribution 學下來，而是在不同的可能的點中不斷震盪。

但是幸好，von Neumann 說：如果兩個玩家都有『mixed strategies』，則這個遊戲就會有平衡點。『mixed strategies』很簡短地說，就是現在玩家們手上的策略形成一個分佈，因此不同策略被挑到的機率不一樣。如果現在有玩家 A、B，a 是玩家 A 從某個策略分佈 ( $S_A$ 選出的策略；B 也同樣有 b 和 $S_B$ 。

在『mixed strategies』中有平衡點的意思是：存在一個數字 $V$ ，和一組策略分佈 ( $S_A,S_B$ ) ，使得

所有 a，面對 B 的策略的期望值都不大於 $V$ ；
所有 b，面對 A 的策略的期望值都不小於 $V$ ；

不過上面的平衡點是發生在 Generator 和 Discriminator 都有無限多個情況下。在實務上，只有「有限多個 generator 」和「有限多個 discriminator 」( 甚至只有一個 )，而且我們很貪心，希望 generator 總是贏。因此我們只能得到所謂的 $\epsilon$ -approximate equilibrium，也就是容許 $[V-\epsilon, V+\epsilon]$ 的差距。

這篇論文的最終目標是用一個稍微大一點點的 generator 去模擬「有限多個 $n$ -parameter 的 generator 的『mixed strategies』」，然後對上一個 $n$ -parameter 的 discriminator。論文中證明：

這個有『mixed strategies』的 generator ，和一個最佳解就只能是隨便亂猜的 discriminator 可以形成一個 $\epsilon$ -approximate equilibrium。也就是我們可以製造一個 generator 和 discriminator 有近似平衡點，而且 generator 永遠都會贏的情況！

如果只想知道文章開頭提問的答案，看到這裡就可以結束了 XD ，下面只是簡單提一下如何製造這個 generator 的概念。

如何製造一個 $\epsilon$ -approximate equilibrium 的情況？

無限多的 generator v.s. 一個 discriminator

如果有無限多的 generator 而且可以將它們混合，那很顯然的這個混合版的 generator 一定超強，因為機率上，『對於任何一個 distribution $P_{real}$ 都能用無限多個 Gaussian distribution 去任意近似它』，因此顯然的就算這個 discriminator 超強〈可以是任意 Lipschitz function 〉，它還是無法分辨。

有限多的 generator v.s. 一個 discriminator

如果 generator 跟 discriminator 的可調參數都只有 n 個。則從 $\epsilon$ -approximate equilibrium 的討論我們知道，只要混合 $\tilde{O}(n log(n/\epsilon)/\epsilon^2)$ 個 generator ，那 discriminator 就無法分辨這些 generator 產生出來的distribution $P_G$ 和 $P_{real}$ ，就算此時有限個 generator 產生的 $P_G$ 和 $P_{real}$ 有差距。

一個超強 generator v.s. 一個 discriminator

但是公然的用多個 generator 去打一個 discriminator 顯然太不公平了，所以只好想辦法做出單一一個 generator ，而這個超強 generator 其實就是要想辦法『模擬有限多的 generator 』。如果現在有 $G_1, \cdots G_T$ T個 generator，則每次收到一個 input $z$ ，就讓這 T 個 generator 都吃進這個 input ，但是只有一個 generator 可以繼續往下跑。那這個 generator 怎麼選？很簡單，就是 uniformly 隨機選 XD 總之我們可以花比單一個 generator 僅僅多一層的 neural network，就能變成一個可模擬多個 generator 的超強產生器了！

這些問題筆者猜測其實很多人質疑過，但直到 2017 才由 Arora、Rong Ge 等人提出三篇論文，用嚴謹的數學證明、以及實驗驗證來給這些問題一些答案。而當然這方面的研究並不是到這裡就結束了，還有很多疑惑需要更多人幫忙解決，畢竟 GAN 這個模型發展到現在也才三年，還在一個不成熟的時期。

GAN系列文(4)–Generalization and Equilibrium in GANs